
The Competition on the Mathematics of Information (CMI) is a mathematics competition for senior secondary school students organized by the Mathematics and Information Engineering Programme (a joint programme offered by the Departments of Mathematics and Information Engineering, CUHK) at the Chinese University of Hong Kong. The competition will consist of 4 – 5 challenging math questions, with interesting connections with information sciences.
News
- [21 June 2024] Here is the details of the Award Ceremony:
Date: 28 June 2024 (Friday)
Time: 3:00 PM
Venue: Room 801, 8th Floor, Ho Sin Hang Engineering Building, The Chinese University of Hong Kong - [24 April 2024] Sorry for keeping you waiting! The competition results are now available. Please check the list of awardees here.
The award ceremony is tentatively scheduled for Friday, June 28, 2024. We will send out invitations to awardees shortly. Heartfelt congratulations to all the awardees! - [19 February 2024] Thank you for the registration. The competition is confirmed to be held at Lecture Theatre 1, Yasumoto International Academic Park (YIA) at the Chinese University of Hong Kong on 24 February 2024 (Saturday).
The Competition 2024
| Date | |
| Time | 9:30 am – 12:30 pm |
| Venue | Lecture Theatre 1 Yasumoto International Academic Park (YIA) The Chinese University of Hong Kong Campus Map |
| Eligibility | Secondary school students in Hong Kong. Previous exposure to calculus is recommended. |
Aim
To recognize talented students in mathematics and information science.
Target Group
Secondary school students in Hong Kong. Previous exposure to calculus is recommended.
Prizes
First Place
Second Place
Third Place
Certificates of distinction will be awarded to high performers. Award ceremony will be held on a separate date.
Registration Deadline
Extended to
13th February, 2024 (Tuesday) 23:59
Rules
- The competition will be in the form of an examination, with a time limit of 3 hours.
- This is an individual competition. Contestants must not communicate with anyone other than invigilators during the competition.
- Contestants should bring their HKID cards for identification purposes.
- Contestants are allowed to bring pens, pencils, rulers, erasers and correction tapes or fluid. No other items (e.g. calculators, phones, books, papers) are allowed during the competition. Contestants should bring their own stationery.
- Contestants must arrive before 9:15am.
- The exam paper will be in English.
- Should you have any questions during the competition, please raise your hand. An invigilator will come to assist you.
- Photos may be taken during the competition for promotional purposes.
- If the competition is postponed or cancelled, it will be announced on the website , and via email to the registered contestants. Please check our website periodically for updated information.
- The award ceremony will be held on a later date announced on our website.
Sample Problem
You are trying to communicate a message to your friend. There is a room with 8 light bulbs, where each of them can be switched on or off individually. You enter the room, switch some light bulbs on or off, and leave the room. Your friend then view the room through a window and attempts to find out the message you are trying to convey. You and your friend can agree on a strategy before you enter the room. If all light bulbs are working correctly, you can convey a message with 28 = 256 possibilities, such as an integer in the range 0,1,…,255, by switching the light bulbs on or off according to the binary representation of the integer.
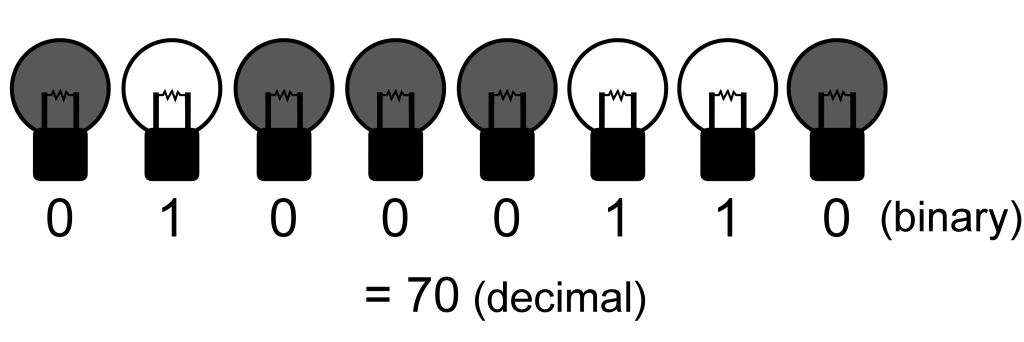
1. Now, both of you know that exactly one of the light bulbs is faulty, i.e., it is stuck at either on or off. You can know which light bulb is faulty by trying to switch the light bulbs on and off. If your friend knows which light bulb is faulty as well, you can convey a message with 27 = 128 possibilities simply by ignoring the faulty light bulb. However, your friend does not know which light bulb is faulty.
How many different possibilities can you convey? Can you still convey a message with 128 possibilities?
2. Suppose now both of you know that there are exactly two faulty light bulbs. How many different possibilities can you convey?
Bibliographic note: This strategy can be applied to store information in memory cells, where some cells are defective. It has been studied in:
A. V. Kuznetsov and B. S. Tsybakov, “Coding in a memory with defective cells,” Probl. Peredachi Inf., vol. 10, no. 2, pp. 52–60, 1974.
S. I. Gel’fand and M. S. Pinsker, “Coding for channel with random parameters,” Probl. Contr. and Inf. Theory, vol. 9, no. 1, pp. 19–31, 1980.
C. Heegard and A. El Gamal, “On the capacity of computer memory with defects,” IEEE Trans. Inf. Theory, vol. 29, no. 5, pp. 731-739, 1983.
Apply
Thank you for the nomination and registration. The application deadline has passed.
