The Competition on the Mathematics of Information (CMI) is a mathematics competition for senior secondary school students organized by the Mathematics and Information Engineering Programme (a joint programme offered by the Departments of Mathematics and Information Engineering, CUHK) at the Chinese University of Hong Kong. The competition will consist of 4 – 5 challenging math questions, with interesting connections with information sciences.
News
- [15 February 2025] Thank you for all of the school nominations and applicant registrations. The registration deadline has now closed. We will send out confirmation emails to all successful registrants of this competition within one week.
- [6 January 2025] The CMI 2025 website is online. We accept school nomination and online registration till 15 February 2025 (Saturday).
The Competition 2025
| Date | 1 March 2025 (Saturday) |
| Time | 9:30 am – 12:30 pm |
| Venue | Lecture Theatre 1 Yasumoto International Academic Park (YIA) The Chinese University of Hong Kong Campus Map |
| Eligibility | Secondary school students in Hong Kong. Previous exposure to calculus is recommended. |
Aim
To recognize talented students in mathematics and information science.
Target Group
Secondary school students in Hong Kong. Previous exposure to calculus is recommended.
Prizes
First Place
Second Place
Third Place
Certificates of distinction will be awarded to high performers. Award ceremony will be held on a separate date.
Registration Deadline
15th February, 2025 (Saturday) 23:59
Rules
- The competition will be in the form of an examination, with a time limit of 3 hours.
- This is an individual competition. Contestants must not communicate with anyone other than invigilators during the competition.
- Contestants should bring their HKID cards for identification purposes.
- Contestants are allowed to bring pens, pencils, rulers, erasers and correction tapes or fluid. No other items (e.g. calculators, phones, books, papers) are allowed during the competition. Contestants should bring their own stationery.
- Contestants must arrive before 9:15am.
- The exam paper will be in English.
- Should you have any questions during the competition, please raise your hand. An invigilator will come to assist you.
- Photos may be taken during the competition for promotional purposes.
- If the competition is postponed or cancelled, it will be announced on the website , and via email to the registered contestants. Please check our website periodically for updated information.
- The award ceremony will be held on a later date announced on our website.
Sample Problem
You are trying to communicate a message to your friend. There is a room with 8 light bulbs, where each of them can be switched on or off individually. You enter the room, switch some light bulbs on or off, and leave the room. Your friend then view the room through a window and attempts to find out the message you are trying to convey. You and your friend can agree on a strategy before you enter the room. If all light bulbs are working correctly, you can convey a message with 28 = 256 possibilities, such as an integer in the range 0,1,…,255, by switching the light bulbs on or off according to the binary representation of the integer.
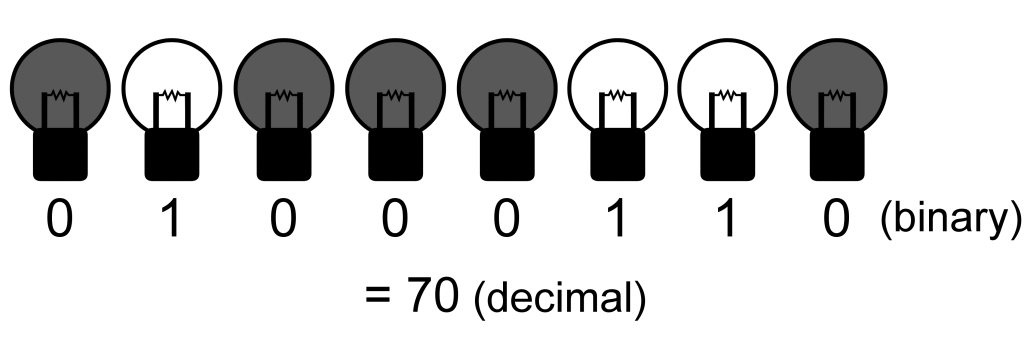
1. Now, both of you know that exactly one of the light bulbs is faulty, i.e., it is stuck at either on or off. You can know which light bulb is faulty by trying to switch the light bulbs on and off. If your friend knows which light bulb is faulty as well, you can convey a message with 27 = 128 possibilities simply by ignoring the faulty light bulb. However, your friend does not know which light bulb is faulty.
How many different possibilities can you convey? Can you still convey a message with 128 possibilities?
2. Suppose now both of you know that there are exactly two faulty light bulbs. How many different possibilities can you convey?
Bibliographic note: This strategy can be applied to store information in memory cells, where some cells are defective. It has been studied in:
A. V. Kuznetsov and B. S. Tsybakov, “Coding in a memory with defective cells,” Probl. Peredachi Inf., vol. 10, no. 2, pp. 52–60, 1974.
S. I. Gel’fand and M. S. Pinsker, “Coding for channel with random parameters,” Probl. Contr. and Inf. Theory, vol. 9, no. 1, pp. 19–31, 1980.
C. Heegard and A. El Gamal, “On the capacity of computer memory with defects,” IEEE Trans. Inf. Theory, vol. 29, no. 5, pp. 731-739, 1983.
Apply
How to enter the competition? We accept the following channels:
- School Nomination
We welcome secondary school principals to nominate up to 10 talented students to join this competition. Please download the nomination form here and send the completed form to Ms Winnie Chan. - Student Application
Secondary school students who want to challenge themselves may directly register at https://cloud.itsc.cuhk.edu.hk/webform/view.php?id=13661982 - The application deadline for both channels will be on 15 February, 2025 (Saturday) 23:59.
- Successful applicants will be notified within a week after the deadline.
- The organizers reserve the right to limit the number of contestants per school.
- [Application closed — as of 15 February 2025]