Get to know MIEG – A Conversation with AI
Question 1: Why is knowledge of Mathematics important for Research in Information Theory, Coding Theory, Wireless Networks, and Computer Networks?
Perplexity’s answer:
A strong knowledge of mathematics is essential for research in information theory, coding theory, wireless networks, and computer networks due to several fundamental reasons:
- These fields are rooted in mathematical concepts like probability theory, stochastic processes, algebra, and discrete mathematics that form the theoretical foundation for analyzing, modeling, and optimizing complex systems.
- In information theory, mathematics enables the precise definition and quantification of information, uncertainty, and communication limits through core measures such as entropy and mutual information. This mathematical rigor ensures results are exact and universally applicable.
- Coding theory heavily relies on algebra and combinatorics to design error-correcting codes, which allow reliable data transmission and storage despite noise in communication channels—critical in wireless and computer networks.
- Wireless and computer networks use mathematical tools like graph theory, optimization, probability, and linear algebra to model network architectures, optimize routing and resource allocation, and analyze performance under uncertainty and interference.
- Mathematics develops logical thinking and problem-solving skills, which are indispensable for rigorously designing algorithms, proving their correctness, and ensuring systems operate efficiently and securely.
In summary, mathematics provides the precise language and methodological tools necessary to understand, model, optimize, and innovate in information theory, coding, and networking research. Without it, advancements in these highly technical and mathematically intensive fields would not be possible.
Comment by the MIEG programme:
- This answer is spot on for a lay person. For a more knowledgeable person, we urge you to look at the further probing questions.
Question 2: What are mathematical areas used for research in Information Theory, Coding Theory, Wireless Networks, and Computer Networks?
Perplexity’s answer:
- Probability Theory and Stochastic Processes
- Fundamental for modeling uncertainty, noise, and random signals in communication systems.
- Enables quantification of information measures like entropy and mutual information, which capture uncertainty and information content of random sources and channels.
- Used extensively in performance analysis of wireless channels and network traffic modeling.
- Information Theory Mathematics
- Centers on concepts such as entropy, joint and conditional entropy, mutual information, relative entropy, and channel capacity.
- Incorporates Shannon’s theorems including source coding theorem, channel coding theorem, and rate–distortion theory, quantifying theoretical limits on data compression and reliable transmission over noisy channels.
- Uses asymptotic equipartition property and bounds to analyze long sequences of data.
- Algebra and Finite Fields (Galois Fields)
- Crucial for coding theory, particularly in designing error-correcting codes like Reed-Solomon, BCH, cyclic codes, and convolutional codes.
- Abstract algebra concepts such as groups, rings, and fields provide the structure to build and analyze these codes.
- Enables construction of linear codes and decoding algorithms that correct errors introduced by noisy transmission.
- Combinatorics
- Used for counting and arranging codewords, analyzing code distances (e.g., Hamming distance), and designing codes with optimal properties.
- Supports enumeration of error patterns and performance bounds in coding theory.
- Linear Algebra
- Applied in representing codes, network topologies (via adjacency matrices), and solving systems of linear equations in network coding.
- Supports optimization in resource allocation and signal processing in wireless networks.
- Graph Theory
- Essential for modeling networks including routing, flow, and connectivity problems.
- Used in topology control, network design, and optimization of communication paths.
- Optimization Theory
- Used to maximize data rates, minimize latency or power consumption, optimize scheduling, resource allocation, and other network operations.
- Measure Theory and Real Analysis (Advanced)
- Forms the rigorous foundation of probability and information theory, especially in continuous alphabets and channels.
- Supports the definition and proof of channel coding theorems and capacity results.
These mathematical foundations collectively enable precise modeling, analysis, and design of communication systems and networks, supporting advancements from theoretical limits to practical algorithms and protocols.
Comment by the MIEG programme:
This answer is again rather comprehensive from a big picture. However, it does miss some deeper links, for example, connections to differential geometry.
Question 3: Is Information Theory a Mathematical Discipline?
Perplexity’s answer:
Information theory must be considered a mathematical discipline because it fundamentally revolves around the precise quantification, modeling, and analysis of information using mathematical concepts, structures, and proofs. Originally established by Claude Shannon in the 1940s, information theory formalizes the concept of information through mathematical measures such as entropy, mutual information, channel capacity, and rate-distortion functions. These concepts allow for rigorous theoretical limits on data compression, transmission, and reliable communication over noisy channels, expressed as mathematical theorems and inequalities.
The discipline’s foundations are axiomatically structured with a system of ontological and axiological principles, systematically defining what information is and how it can be measured and manipulated. This approach parallels how mathematics builds theories from fundamental concepts through formal definitions and logical deductions. Information theory also integrates key branches of mathematics such as probability theory, combinatorics, algebra, and optimization, applying these rigorously to communication and coding problems.
Additionally, the strong mathematical basis enables:
- Constructing error-correcting codes and algorithms that approach theoretical performance limits.
- Modeling uncertainty and noise in communication channels through stochastic processes.
- Defining rigorous performance metrics grounded in measurable quantities.
- Providing universal frameworks applicable across diverse fields, from electronic communications to cryptography, neuroscience, and statistical inference.
Without its mathematical grounding, information theory would lack the precision, universality, and predictive power essential to drive the technological advances it has enabled. Thus, information theory stands as a core mathematical discipline dedicated to the study of information in quantitative, formal, and foundational terms.
Comment by the MIEG programme:
Again this is a fairly well-reasoned answer.
Question 4: What are some important Contributions of Information and Coding Theory to Everyday Engineering Applications?
Perplexity’s answer:
- Data compression and source coding: Information theory provides fundamental limits and algorithms for compressing data efficiently, enabling practical technologies like ZIP files, audio/video compression, and storage optimization.
- Error detection and correction: Coding theory designs error-correcting codes (such as Reed-Solomon and convolutional codes) that allow reliable data transmission and storage, even in noisy environments like wireless and computer networks.
- Reliable communication over noisy channels: Information theory establishes channel capacity limits and designs coding schemes that approach these limits, crucial for mobile communications, satellite links, and internet data transfer.
- Cryptography and secure communication: Information-theoretic concepts underpin cryptosystems, ensuring secure and private transmission of data in everyday encryption technologies.
- Network design and optimization: Graph theory and optimization methods drawn from these theories help model, optimize, and manage routing, resource allocation, and network architectures in wireless and computer networks.
These contributions make possible many common technologies such as internet access, mobile telephony, digital media streaming, and secure online transactions.
Comment by the MIEG programme:
This answer is again rather comprehensive from a big picture.
Question 5: Currently, what are some important Areas of Research in Information and Coding Theory?
Perplexity’s answer:
- Advanced Coding Technology: Research on channel coding beyond 5G technologies and new coding methods to improve communication efficiency and reliability.
- Semantic Communication: Developing theories around semantic information, including rate-distortion approaches that focus on meaning and content relevance rather than just bit accuracy.
- Cryptography and Information-Theoretic Security: The intersection of information theory with secure communication, including information-theoretic cryptography.
- Quantum Information Theory: Exploring quantum communication, quantum coding, and new applications at the intersection of quantum mechanics and information theory.
- Machine Learning and Pattern Recognition: Applying information theory principles to improve learning algorithms and data processing.
- Energy-Efficient Communication Systems: Optimizing systems such as hybrid beamforming for integrated sensing and communication to reduce energy use.
- Privacy and Data Estimation: Research on locally private distribution estimation and block designs for data privacy.
These topics are actively discussed in forums such as the 2025 Asia Pacific Workshop on Data Science and Information Theory, IEEE Information Theory Society events, and recent academic publications in the field. This reflects a broad trend towards applications in next-generation communications, security, semantics, and interdisciplinary approaches combining information theory with AI and quantum technologies.
Question 6: Currently what are some important Areas of Research in Wireless and Computer Networks?
Perplexity’s answer:
5G and Beyond (6G) Technology: Research focuses on expanding 5G capabilities and early development of 6G, which promises ultra-high speeds (up to 1 terabit per second), ultra-low latency, and AI-driven adaptive networks for applications like autonomous vehicles and smart infrastructure.
Wi-Fi 7 and Advanced Wireless Standards: Wi-Fi 7 brings much faster speeds (over 40 Gbps), lower latency, and better handling of many simultaneous devices, driven by innovations like multi-link operation and wider channels. This supports smart cities, enterprise networks, healthcare data exchange, and IoT devices.
AI-Driven Network Optimization: Using artificial intelligence and machine learning for autonomous network management, resource allocation, predictive analytics, and energy optimization is a major trend. AI helps networks dynamically respond to traffic demands and disruptions.
Internet of Things (IoT) Connectivity: Expanding wireless networks to support billions of connected devices in smart homes, factories, wearables, and city infrastructure is critical, requiring scalable, robust, and secure network designs.
Network Slicing and Private Networks: Research on 5G network slicing enables multiple virtual networks to operate on a single physical infrastructure tailored for specific applications or enterprises. Private wireless deployments also grow for enhanced security and performance.
Security and Cybersecurity in Networks: With more connected devices and critical applications, securing wireless and computer networks against evolving cyber threats is increasingly important, including studies on secure protocols and threat detection using AI.
New Spectrum Management and Infrastructure: Optimizing spectrum usage, deploying small cells, neutral host solutions, and expanding network coverage to underserved areas, including rural connectivity, remain key research and deployment focuses.
Integration of Non-Terrestrial Networks: Research on satellite and other non-terrestrial systems complements terrestrial networks to ensure global coverage and service reliability.
These research areas collectively aim to improve network speed, reliability, security, energy efficiency, and scalability to meet the demands of futuristic applications in communication, computing, and the digital economy.
Question 7: What are some fundamental Open Problems in Information and Coding Theory?
Perplexity’s answer:
Universal constraints and new inequalities in information theory: Understanding and proving new general information inequalities, especially involving algorithmic information theory quantities like mutual information and its generalizations. This includes developing computer-assisted proof techniques for discovering universal laws applicable across communication complexity and secret sharing.
Open problems in quantum information theory related to coding: Such as the existence of special measurement sets (symmetric informationally complete measurements), mutually unbiased bases in certain dimensions, and the nature of bound entangled states. These problems also have implications for quantum coding.
Theoretical challenges in learning and coding: Theoretical aspects of learnability, optimization, and complexity in algorithms that intersect with information theory remain open in areas such as network coding, data compression, and privacy.
Phase retrieval and signal reconstruction problems: Open problems related to phase retrieval and signal reconstruction codes that are relevant to information theory and coding.
Secure communication with new constraints: Designing secure communication and secret sharing schemes under practical limitations, such as rate-limited public communication and correlated randomness, remain open areas.
These open problems are actively discussed in major conferences like IEEE ISIT, COLT, and workshops focusing on quantum information, data science, and algorithmic information theory.
Question 8: What are some important Open Problems in Network Information Theory?
Perplexity’s answer:
Capacity of a general wireless network: The exact capacity (maximum transmission rate) for general wireless networks remains unknown beyond some special cases like AWGN channels and fading channels.
Capacity of the broadcast channel: Determining the ultimate capacity when a single transmitter sends information to multiple receivers is an open problem in general, with only certain cases solved.
Capacity of the interference channel (two-user case): The capacity region when two transmitters interfere with each other is unknown in general, though some regimes like strong interference and certain deterministic models are characterized.
Capacity of the two-way channel: The exact capacity when communication occurs simultaneously in both directions over a channel is still an open question.
Secure communication and secrecy capacity: Understanding the fundamental limits of secure communication in network scenarios, especially under complex interference and multiuser constraints.
Distributed source coding with distortion constraints: How to compress correlated sources separately but efficiently remains unknown in general.
Queue-channel feedback capacity: Whether feedback increases capacity under realistic service time distributions or queue policies is unsettled.
These problems pertain to fundamental limits on how efficiently and reliably information can be transmitted, shared, and secured in complex networked environments, which go beyond classical single-link channel models.
They are actively researched in the information theory community and discussed in conferences like IEEE ISIT and workshops on network information theory.
Overview
Mathematics and Information Engineering (MIEG) is a rigorous and selective programme designed to equip students with solid fundamental knowledge in mathematics, information and computer sciences.
The following shows a graphical presentation of the MIEG programme contents and its outcomes:
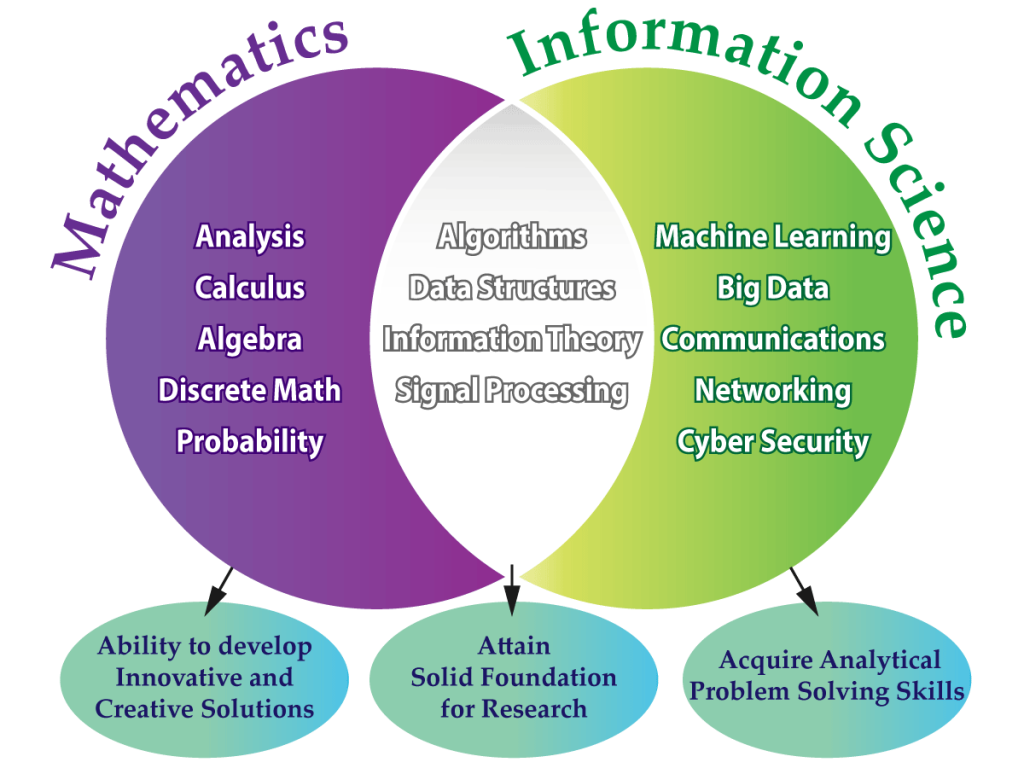
Graduates from this programme routinely go for postgraduate studies at the top universities or pursue independent research or careers in various sectors.
MIEG is an interdisciplinary programme jointly offered by the Faculty of Science and the Faculty of Engineering, with the Department of Mathematics and the Department of Information Engineering responsible for its management and actual running. The students of this programme will have an exposure to both mathematical rigour (the math classes are shared with Math majors) and engineering intuition in the information and computer sciences.
Some of Our Graduates

YU Tingyang
(2023)
PhD in Communication and Computer Sciences at EPFL

LIU Yinyin Jessica (2022)
MSc in EECS at UC Berkeley

WOO Pui Yang Anna (2022)
PhD in CSE at University of Michigan

HEGAZY, Mahmoud (2022)
PhD in Data & Artificial Intelligence at Institut Polytechnique de Paris
Programme Objectives and Outcomes
Our Programme aims to train our students to have a good understanding of fundamental knowledge and objectives. The following achievements are expected:
- The graduates will have had solid mathematical and engineering knowledge for further studies at the graduate school level or for performing independent research work in engineering, industry, or economic sectors.
- The graduates will have the skills to excel in professional positions in organizations that research, design, develop, deploy, or employ information systems/networks/services.
- The graduates will have acquired the ability to continue their personal development through professional studies and life-long learning, and are already acquainted with the benefits of interdisciplinary learning.
Learning outcomes define the graduate capabilities needed to achieve the programme objectives stated. The following lists the 7 learning outcomes of the programme:
- Foundations:
Students will have gained an understanding of the fundamentals of mathematics, science, and engineering and be able to apply them to the research, design, analysis, and implementation of engineering systems.
- Breadth:
Students will have gained exposure to and understand the impact of other science and engineering areas as well as non-engineering areas such as social, economic, environmental, health and safety issues.
- Depth:
Students will have possessed sound knowledge in mathematical analysis, linear algebra, communications and networking, and software development.
- Curiosity:
Students will have possessed the ability to appreciate the value of and develop the ability for lifelong learning.
- Creativity:
Students will have developed problem-solving skills and the ability to innovate new engineering solutions.
- Integrity:
Students will have gained an understanding of the importance of professional, social, and ethical responsibilities in engineering practice.
- Communication Skills:
Students will have developed the skills to communicate effectively both orally and in writing.



